Artificial Intelligence

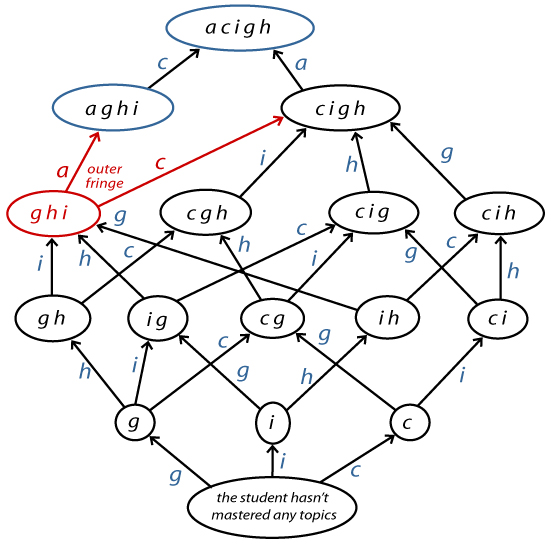
Pinpointing the Current Knowledge State of Each Student

The artificial intelligence of the ALEKS system lies in its learning and assessment engines. The output of these engines is not a numerical aptitude score or an achievement level. Rather, it is a knowledge state, describing all the skills and concepts mastered so far by a student in a given subject, such as Algebra 1 or General Chemistry. This means specifying each and every topic that the student is capable of solving (and therefore all the topics the student is not yet capable of solving). ²

All the feasible knowledge states for a given subject are organized into a learning space, which is a mathematical structure specifying the precedence relation between such knowledge states; that is, which knowledge states may precede or follow other states in the learning process. Figure 1 depicts a miniature learning space formed by five topics labeled a, c, g, h, and i. Each ellipse represents one of 16 feasible knowledge states in this miniature learning space ³. The blank circle at the bottom represents the empty knowledge state (i.e. the student hasn’t mastered any of the five topics). Learning proceeds from bottom to top, the topics being mastered successively. The knowledge state represented by the red ellipse contains the items g, h, and i; topics a and c form the topics the student is highly likely to be ready to learn next. In fact, every knowledge state automatically specifies the collection of topics that the student is ready to learn at that moment. These topics form the outer fringe of the student’s knowledge state; in ALEKS, we call these topics the "ready to learn."

Figure 1

Drawing the same type of graph for ALEKS Beginning Algebra, for example, which contains hundreds of topics, is not only daunting, but impractical. Some idea of the difficulty is conveyed by the graph in Figure 2, which represents the learning space of just 45 of the topics in Beginning Algebra. Every point in the graph represents a knowledge state; the colors of the lines linking the states correspond to the various topics. However, the assessment and learning engines within ALEKS are capable of efficiently managing such enormous structures.

Figure 2

Another example, ALEKS Algebra 2, is currently a domain of 586 topics; a typical implementation uses 384 of them. This gives rise to over a trillion feasible knowledge states. The mathematical language of Knowledge Space Theory has made possible the creation of ALEKS computer algorithms that rapidly and efficiently search and apply the feasible knowledge states in a particular subject to each individual student’s behavior during learning and assessment.